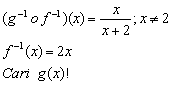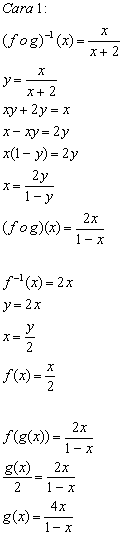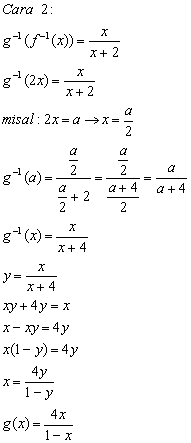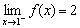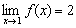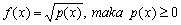Pengertian tentang limit dapat diperoleh dengan melihat contoh berikut ini.
Contoh: Perhatikan fungsi
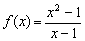
untuk nilai x yang mendekati 1
Gambar grafiknya:

Dari gambar dan tabel dapat disimpulkan:
→ Jika x mendekati 1 dari kiri, maka nilai f(x) mendekati 2
→ Jika x mendekati 1 dari kanan, maka nilai f(x) mendekati 2
→ Jadi, jika x mendekati 1, maka nilai f(x) mendekati 2
Teorema:

Jika limit kiri dan limit kanan tidak sama, maka nilai limitnya tidak ada
Hasil limit tidak boleh bentuk tak tentu:

Sifat-Sifat Limit
Contoh:
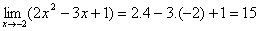
2. Pemfaktoran (biasanya untuk bentuk 0/0)
Contoh:
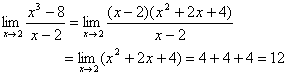
Ingat:
3. Dikali sekawan (jika ada bentuk akar)
Contoh:

4. Untuk limit tak terhingga:
→ Jika bentuknya sudah pecahan: dibagi pangkat tertinggi
→ Jika bentuknya belum pecahan: dikali sekawan, baru dibagi pangkat tertinggi
Sifat operasi dengan ∞:

Contoh:

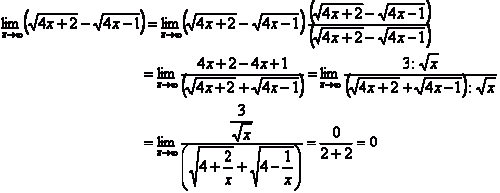
Cara cepat!
→ Untuk bentuk pecahan:
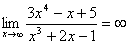
Contoh 2:

Contoh 3:
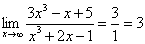
→ Untuk bentuk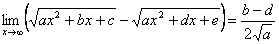
Contoh:
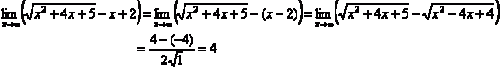
5. Limit trigonometri:

Untuk cosinus:
1 – cos ax = 2 sin2 ½ ax (dari rumus cos 2x)
cos ax – 1 = –2 sin2 ½ ax (dari rumus cos 2x)
1 – cos2ax = sin2ax (dari sin2x + cos2x = 1)
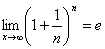
e = 2,718281828…
Rumus-rumus pengembangannya:

1. f(a) ada (dapat dihitung/real)
2.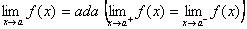
3.
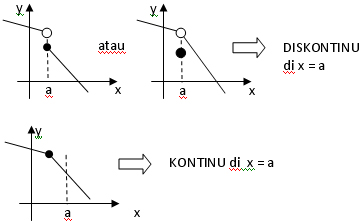
Ilustrasi:
Contoh: Perhatikan fungsi
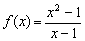
untuk nilai x yang mendekati 1
| x | 0 | 0,9 | 0,95 | 0,98 | … | 1,0001 | 1,0005 | 1,05 | 1,1 |
| f(x) | 1 | 1,9 | 1,95 | 1,98 | … | 2,0001 | 2,0005 | 2,05 | 2,1 |

Dari gambar dan tabel dapat disimpulkan:
→ Jika x mendekati 1 dari kiri, maka nilai f(x) mendekati 2
→ Jika x mendekati 1 dari kanan, maka nilai f(x) mendekati 2
→ Jadi, jika x mendekati 1, maka nilai f(x) mendekati 2
Teorema:

Jika limit kiri dan limit kanan tidak sama, maka nilai limitnya tidak ada
Hasil limit tidak boleh bentuk tak tentu:

Sifat-Sifat Limit
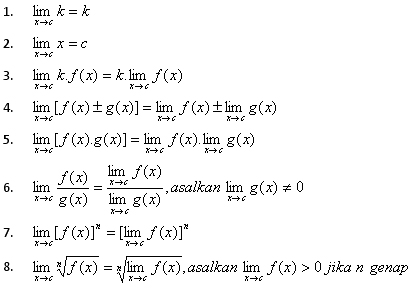
Cara Penyelesaian Limit dengan Perhitungan:
1. Substitusi langsungContoh:
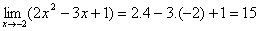
2. Pemfaktoran (biasanya untuk bentuk 0/0)
Contoh:
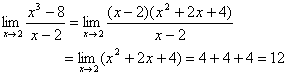
Ingat:
(a2 – b2) = (a – b)(a + b)
(a3 + b3) = (a + b)(a2 – ab + b2)
(a3 – b3) = (a – b)(a2 + ab + b2)
Contoh:
4. Untuk limit tak terhingga:
→ Jika bentuknya sudah pecahan: dibagi pangkat tertinggi
→ Jika bentuknya belum pecahan: dikali sekawan, baru dibagi pangkat tertinggi
Sifat operasi dengan ∞:

Contoh:

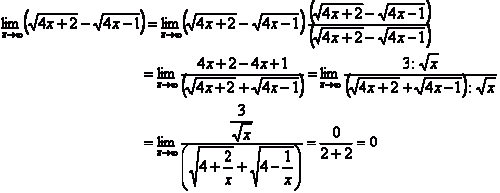
Cara cepat!
→ Untuk bentuk pecahan:
- Jika pangkat pembilang (atas) > penyebut (bawah), hasil =∞
- Jika pangkat pembilang (atas) < penyebut (bawah), hasil =0
- Jika pangkat pembilang (atas) = penyebut (bawah), hasil =koefisien pangkat tertinggi atas : koefisien pangkat tertinggi bawah
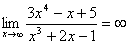
Contoh 2:

Contoh 3:
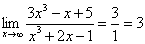
→ Untuk bentuk
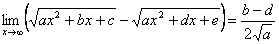
Contoh:
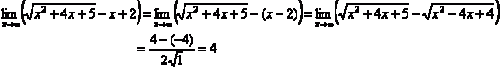
5. Limit trigonometri:

Untuk cosinus:
1 – cos ax = 2 sin2 ½ ax (dari rumus cos 2x)
cos ax – 1 = –2 sin2 ½ ax (dari rumus cos 2x)
1 – cos2ax = sin2ax (dari sin2x + cos2x = 1)
Bilangan e
Bilangan e didapat dari: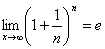
e = 2,718281828…
Rumus-rumus pengembangannya:

Kontinuitas
Suatu fungsi kontinu di x = a jika:1. f(a) ada (dapat dihitung/real)
2.
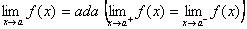
3.

Ilustrasi:

Fungsi
Pengertian
Pasangan terurutContoh:
A = {1, 2, 3}, B = {4, 5}
Himpunan semua pasangan terurut dari A dan B adalah:
{(1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5)}
Relasi
Relasi adalah himpunan dari pasangan terurut ang memenuhi aturan tertentu
Contoh:
A = {1, 2, 3, 4}, B = {2, 4}
Jika ada relasi R dari A ke B dengan aturan ”faktor dari”, maka himpunan pasangan terurut untuk relasi tersebut adalah:
R = {(1, 2), (1, 4), (2, 2), (2, 4), (4, 4)}
Diagram panahnya:

Fungsi
Fungsi dari A ke B adalah relasi yang memasangkan setiap anggota himpunan A ke hanya satu anggota himpunan B
Notasi fungsi f dari A ke B ditulis f : A → B
A disebut domain (daerah asal)
B disebut kodomain (daerah kawan)
Himpunan bagian dari B yang merupakan hasil dari fungsi A ke B disebut range (daerah hasil)
Fungsi juga dapat dinyatakan dengan lambang f : x → y = f(x)
dimana y = f(x) adalah rumus fungsi dengan x sebagai variabel bebas dan y sebagai variabel terikat (tak bebas)
Contoh:
 Untuk fungsi yang digambarkan dalam diagram panah di atas:
Untuk fungsi yang digambarkan dalam diagram panah di atas:Domain = Df = {1, 2, 3, 4}
Range = Rf = {2, 4}
Menentukan Daerah Asal Fungsi
Agar suatu fungsi terdefinisi (mempunyai daerah hasil di himpunan bilangan real), maka ada beberapa syarat yang harus dipenuhi.1. Fungsi di dalam akar
2. Fungsi pecahan
3. Fungsi dimana penyebutnya adalah fungsi lain dalam bentuk akar
4. Fungsi logaritma
Contoh:
Daerah asal untuk fungsi

adalah:
x2 + 3x – 4 > 0
(x + 4)(x – 1) > 0
Pembuat nol: x = –4 dan x = 1
Jika x = 0 maka hasilnya 02 + 3.0 – 4 = –4 (negatif)

Jadi Df = {x | x < –4 atau x > 1}
Aljabar Fungsi
Jika f : x → f(x) dan g : x → g(x) maka:Daerah asalnya:
Df+g, Df–g, Df×g = Df ∩ Dg (irisan dari Df dan Dg)
Df/g = Df ∩ Dg dan g(x) ≠ 0
Komposisi fungsi
Notasi:f komposisi g dapat dinyatakan dengan f o g (dapat juga dibaca ”f bundaran g”)
(f o g)(x) = f(g(x)) (g dimasukkan ke f)
Ilustrasi:
 Contoh: f(1) = 2, g(2) = 0, maka (g o f )(1) = g(f(1)) = g(2) = 0
Contoh: f(1) = 2, g(2) = 0, maka (g o f )(1) = g(f(1)) = g(2) = 0Sifat-Sifat Komposisi Fungsi
1. Tidak bersifat komutatif
(f o g)(x) ≠ (g o f)(x)
2. Asosiatif
(f o (g o h))(x) = ((f o g) o h)(x)
3. Terdapat fungsi identitas I(x) = x
(f o I)(x) = (I o f)(x) = f(x)
Contoh 1:
f(x) = 3x + 2
g(x) = 2x + 5
h(x) = x2 – 1
Cari (f o g)(x), (g o f)(x), dan (f o g o h)(x)!
(f o g)(x) = f(g(x)) = f(2x + 5)
= 3(2x + 5) + 2
= 6x + 15 + 2 = 6x + 17
(g o f)(x) = g(f(x)) = g(3x + 2)
= 2(3x + 2) + 5
= 6x + 4 + 5 = 6x + 9
(f o g o h)(x) = f(g(h(x))) = f(g(x2 – 1))
= f(2(x2 – 1) + 5)
= f(2x2 – 2 + 5)
= f(2x2 + 3)
= 3(2x2 + 3) + 2
= 6x2 + 9 + 2 = 6x2 + 11
atau dengan menggunakan rumus (f o g)(x) yang sudah diperoleh sebelumnya,
(f o g o h)(x) = (f o g)(h(x)) = (f o g)(x2 – 1)
= 6(x2 – 1) + 17
= 6x2 – 6 + 17
= 6x2 + 11
Contoh 2:
f(x) = 3x + 2
(f o g)(x) = 6x + 17
Cari g(x)!
(f (g(x)) = 6x + 17
3.g(x) + 2 = 6x + 17
3.g(x) = 6x + 17 – 2
3.g(x) = 6x + 15
g(x) = 2x + 5
Contoh 3:
g(x) = 2x + 5
(f o g)(x) = 6x + 17
Cari f(x)!
f(2x + 5) = 6x + 17
misalkan: 2x + 5 = a → 2x = a – 5
f(a) = 3(a – 5) + 17
f(a) = 3a – 15 + 17
f(a) = 3a + 2
f(x) = 3x + 2
Contoh 4:
f(x) = x2 + 2x + 5
(f o g)(x) = 4x2 – 8x + 8
Cari g(x)!
f(g(x)) = 4x2 – 8x + 8
(g(x))2 + 2g(x) + 5 = 4x2 – 8x + 8
Gunakan cara melengkapkan kuadrat sempurna
(g(x) + 1)2 – 1 + 5 = 4x2 – 8x + 8
(g(x) + 1)2 = 4x2 – 8x + 8 – 4
(g(x) + 1)2 = 4x2 – 8x + 4
(g(x) + 1)2 = (2x – 2)2
g(x) + 1 = 2x – 2 atau g(x) + 1 = –(2x – 2)
g(x) = 2x – 3 atau g(x) = –2x + 3
atau
f(g(x)) = 4x2 – 8x + 8
(g(x))2 + 2g(x) + 5 = 4x2 – 8x + 8
Karena pangkat tertinggi di ruas kanan = 2, maka misalkan g(x) = ax + b
(ax + b)2 + 2(ax + b) + 5 = 4x2 – 8x + 8
a2x2 + 2abx + b2 + 2ax + 2ab + 5 = 4x2 – 8x + 8
a2x2 + (2ab + 2a)x + (b2 + 2ab + 5) = 4x2 – 8x + 8
Samakan koefisien x2 di ruas kiri dan kanan:
a2 = 4 → a = 2 atau a = –2
samakan koefisien x di ruas kiri dan kanan:
untuk a = 2 → 2ab + 2a = –8
4b + 4 = –8
4b = –12 → b = –3
untuk a = –2 → 2ab + 2a = –8
–4b + 4 = –8
–4b = –12 → b = 3
Jadi g(x) = 2x – 3 atau g(x) = –2x + 3
Invers Fungsi
NotasiInvers dari fungsi f(x) dilambangkan dengan f–1 (x)
Ilustrasi
 Contoh: Jika f(2) = 1 maka f–1(1) =2
Contoh: Jika f(2) = 1 maka f–1(1) =2Jika digambar dalam koordinat cartesius, grafik invers fungsi merupakan pencerminan dari grafik fungsinya terhadap garis y = x
 Sifat-Sifat Invers Fungsi:
Sifat-Sifat Invers Fungsi:- (f–1)–1(x) = f(x)
- (f o f–1)(x) = (f–1 o f)(x) = I(x) = x, I = fungsi identitas
- (f o g)–1(x) = (g–1 o f–1)(x)
Mencari invers fungsi
- Nyatakan persamaan fungsinya y = f(x)
- Carilah x dalam y, namai persamaan ini dengan x = f–1(y)
- Ganti x dengan y dan y dengan x, sehingga menjadi y = f–1(x), yang merupakan invers fungsi dari f
f(x) = 3x – 2
invers fungsinya:

Contoh 2:

Cara Cepat!

Contoh 3:
f(x) = x2 – 3x + 4
Invers fungsinya
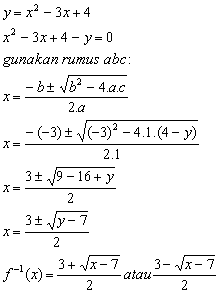
Contoh 4: